How to calculate a regression line in statistics can only be possible if the scatterplot of the two variables shows a linear pattern and correlation between the variables is very strong. But what is a regression line?
A regression line is simply a single line that suits the data. You can determine the best line in terms of having the smallest overall distance from the line to the points. However, the great statistics referred to this technique for finding the best-fitting line a simple linear regression analysis using the least square method. ¬†¬
However, the formula for the regression line is y=mx+b, therefore m is the slope of the line and b is the y-intercept. You can as well make use of this in algebra but statistics lie more on a line. The line is a proof which the data lie assuming a strong linear pattern exists.
Tips
- Thus; the¬†slope¬†of a line is the change in¬†Y¬over the change in¬†X. For example, a slope of 10/3
This simply means that as the value of x increases by 3 units, the value of y moves up by 10 units on average.
- Note that the value of the y-intercept is the value on the y-axis where the line crosses. For instance; in the equation y=3x-6, thus, the line that crosses the y-axis at the value b= -6. Therefore, the coordinates of this point are (0, 6). This is because the line crosses the y-axis, and then the x-value will always be 0.

Having a rethink over and over again just to find from the different lines to see the one that best fits in will not accurately give you the result. There are formulas that can be used to calculate the y-intercept over a distinct slope.
- The mean of the x¬values¬† =

- The mean of their¬values¬† =

- The standard deviation of the x¬values (denoted¬†sx)
- The standard deviation of the y¬values (denoted¬†sy)
- The correlation between X¬and¬†Y¬(denoted¬†r)
How to find the slope of a regression line
The formula to find slope, m, of the best fitting line is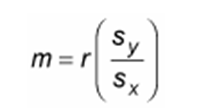
Therefore, r is the correlation between X and Y, while the sx and syis the standard deviations of the x-values and the y-values respectively. Now to get the result of the slope, you can simply divide sy by sx and multiply the result by r
N/B: the slope of the best-fitting line can also be a negative number because the correlation can be a negative number. This indicates that the slope is going downhill.
Also, note that the correlation and the slope of the best-fittings line are not the same. The formula for slope bears the correlation and attaches units to it.
How to find the y-intercept of a regression line
The formula for the y-intercept, (b) of the best-fitting line is
Where m is the slope.
To calculate the y-intercept, b, of the best-fitting line, you have to start by finding the slope, m, of the best-fitting line using the above steps. Then after, to find the y-intercept, you multiply m by 
Note: always calculate the slope before you get to the y-intercept. This is because the y-intercept formula will require you multiple the slope by the above equation. Fig 1


