The Transitive and Substitution Properties
The Transitive properties are the same as algebra. So if you have come in contact with the below formula of algebra then you are not far from the transitive properties. If a = b and b = c, then a = c. it is the same as transitivity. But what then is substitution? Substitution is, a = b and b < c, then a < c. let’s look into the theorems (algebra express in symbols or formula) in full details.
-
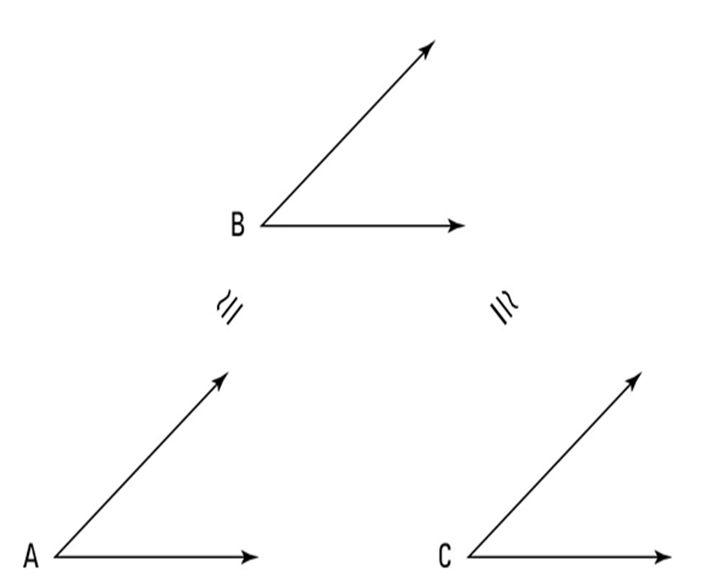
Transitive Property for three segments or angles
This is typically a three segments or angles of transitive whereby if two segments or angles are congruent to the third segment or angle, then they are congruent to each other.
Difference Between Transitive and Substitution Property
https://www.stepbystep.com › difference-between-transi…
Transitive and substitution property are two basic properties of mathematics that are used to solve mathematical expressions. Both these properties have
How can you tell the difference between a transitive and …
https://askinglot.com › how-can-you-tell-the-difference…
Use the Transitive Property as the reason in a proof when the statement on the same line involves congruent things. Use the Substitution …
Reflexive, Symmetric, Transitive, and Substitution Properties
https://www.varsitytutors.com › hotmath_help › topics
Reflexive, Symmetric, Transitive, and Substitution Properties … The Reflexive Property states that for every real number x , x=x . … The Symmetric Property …
2.7 Transitive and Substitution Properties – pacesetters team
https://pacesettersteammath.weebly.com › uploads
In geometry we use the Transitive Property when we have a series of congruent segments or angles that we wish to make or prove congruent. Example: Don’t you …
There is also a transitive property for four segments of angles. Let look at this illustration of the two-segment properties of transitive.
This above figure is a typical illustration of the transitive property of three-segment or angles.
- Transitive Property for Four segments or angles
Assuming two angles are congruent to other congruent angles, thus they are said to be congruent to each other. This is typically how four-segment or angles looks like.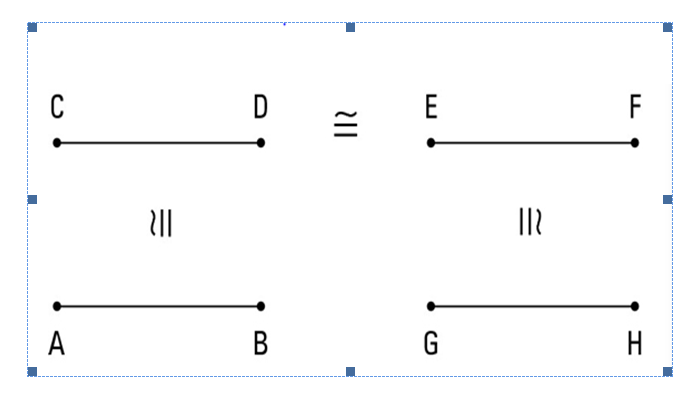
The above illustration is the transitive property for four segments.
Mathematically,
- Substitution Property
Assuming two segments or angle are congruent and as a result, you had a statement involving one of them, thus, you can pull the reversal one and replace the one with the other.
Tip
We have set out tips or guideline that will help you figure out the Transitive and Substitution properties without mixing them up. Therefore, if you are ready, follow the below guide.
- Ensure to use the Transitive properties as the reason in a proof when a statement on the same line involves congruent angles.
- Make use of the substitution property when the statement does not involve a congruence.
Check out for the below proof from a TGFI rectangle!
 Statement 1:
Statement 1:
Thus, the reason for statement 1 is Given.
Statement 2:

The reason for statement 2: whenever two angles form a right angle, it means that they are complimentary. Therefore, it defines complementary.
Statement 3:
Thus, the statement for statement 3 Given.
Statement 4:
What happened over the statement 4 is shows substitution property. Statement 2 and 3; whereby angle 2 replaces 1.
Take a look at the proof for the final segment of the program.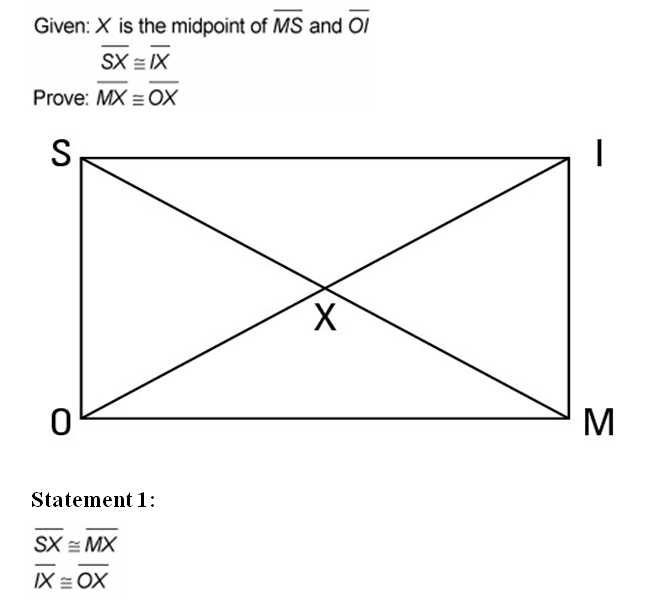
Statement 1:
Reason for statement 1: Given.
Reason for statement 2:�A midpoint divides a segment into two congruent segments.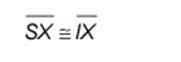
Reason for statement 3:�Given.![]()
Reason for statement 4: Transitive Property (for four segments; statements 2 and 3).


