Properties of Rhombuses, Rectangles, and Squares
Rhombus, rectangle, and square are all special parallelograms. They are also called special because they are special cases of the parallelogram.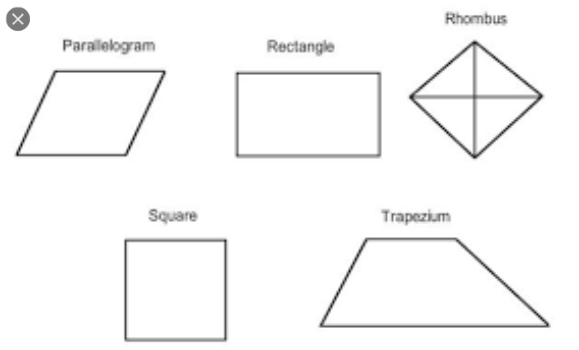
In terms of hierarchy you get to see the below:
Parallelogram – Rectangle – square or Parallelogram – rhombus – square. The same thing runs in the below example.
Mammal – dog – Dalmatian, What this means is that dog is a special type of a mammal, and Dalmatian is a special type of dog.
Below are some properties of the rhombus, rectangle, and square. However, you may get to figure out that rhombuses, rectangle, and square bear the same properties with parallelogram because they are all quadrant of a parallelogram.
Properties of a rhombus are as follows:
Among all the properties, the most important aspect is just what we will take into consideration to see if they posse the same properties. They include the parallel sides, opposite angles, and the consecutive angles.
All the properties of parallelograms are applied. (The parallel sides, opposite angles that are in agreement, and the consecutive angles are supplementary).
- In a rhombus, all sides are congruent by definition.
- The angles are bisected by the diagonals
- The diagonals are perpendicular bisectors of each other.
Properties of the rectangle are as follows:
- Rectangles apply all the properties of parallelogram noting the parallel side opposite sides of the congruent and the diagonals bisect against each other
- All the angles are right angles by definition.
- Thus, the diagonals are in agreement with each other (congruent).
Properties of the square are as follows:
- They apply all the properties of a rhombus. (The parallel sides, the diagonals which are perpendicular bisectors of each other, and diagonals which bisects the angles).
- All the properties of a rectangle apply (the only one that matters here is diagonals are congruent).
- All sides are congruent by definition.
- All angles are right angles by definition.
Now let’s try to work out all that has been said with the below example. Find the measures of angle 1 and angle 2.
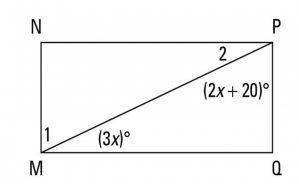
Solution: the total sum of the angles is MNPQ. But angle Q = 90°. Therefore, because there are angle 180 in a triangle, i.e
90° + (3x) ° + (2x+ 20) ° = 180°
3x + 2x + 20 = 90
5x = 70
X = 14
Now put in 14 for X
Therefore,
Find the perimeter of rhombus RHOM

Solution:
Remember that the sides of a rhombus are in agreement. So HO equals X + 2. You will notice that the diagonals are perpendicular, while HBO is a right triangle. With your Pythagorean formulae, you can finish up.
It says;
a^2 + b^2 = c^2
(HB)^2 + (BO) ^2 = (HO) ^2
So you have something like 
Bring together the like terms and set equal to zero:

Factor:
(x – 3)(x + 1) = 0
Use Zero Product Property:
x – 3 = 0 or x + 1 = 0
x�= 3 or x = –1
You can reject x = –1 because that would result in triangle HBO having legs with lengths of –1 and 0.


